Diagnosing some slam hands. Continue reading →
In last Saturday’s club game my partner and I missed a slam at each of the first three tables. We later missed still another slam, but we salvaged one on the very next hand. This may sound like a recipe for a disastrous session, but in fact we enjoyed a 65+% game.
Hand #16: My hand (16 HCP; 6 losers):
♠AKJ864 ♥JT ♦AK2 ♣T5Partner’s hand (12 HCP; 8 losers):
♠T75 ♥A832 ♦65 ♣AKJ3I opened a spade; partner put in the game force with 2♣. I rebid my six-card suit. Partner bid four spades.
The opponents held a motley collection of four queens, the K♥, and the J♦. The finesse of the Q♠ works, but so does the drop. You can ruff the diamond at any time. The club finesse works, and there is no reason not to take it. Three of the seven pairs only took twelve tricks, but it is hard to see a strategy that fails to produce thirteen.
Two popular methods for assessing the viability of slams are Losing Trick Count and Bergen Points. These two approaches were described here.
Losing Trick Count predicts that we would only take ten tricks with these cards. It is easy to understand how the spade loser disappeared, but only one finesse was even available. Even if it had lost, twelve tricks would be easy if the opening lead were anything but a heart. This hand seems to be a good example of the type that LTC systematically undervalues.
How about Bergen Points? My hand upticks to 18 using Bergen’s starting points. I can add two points for the long spades and one for the quality of the spade suit. I have to discount the JT doubleton, at least for the time being. Partner earns an extra point for the quality club suit, and he gets to add a point for his doubleton. That gives him 14 dummy points. We are getting close.
The final adjustment goes to my hand. When he shows support for my suit, I get to add another point for the sixth spade and one point for the doubleton. Together we have 34 Bergen Points, and we should definitely have bid 6♠!
How could we have done it using our bidding methods? I think that my partner’s bidding was fine. Even with the two extra points that Bergen allots him he does not have much to brag about. If anyone is going to go on past game, it would have to be me.
What if I had cue-bid the A♦ after he signed off with 4♠? If I think of my hand as a 20-point powerhouse with two flawed suits rather than as a level-two hand with too many losers, it seems a natural bid. If partner then bids five hearts, I know that he has the ace of hearts, but I can never learn about his club holding. Some play that bidding the heart ace implies that he also has the club ace (because I skipped clubs), but we had never discussed his. Maybe we should.
If I had bid Blackwood instead, however, I would have learned about three cards — the two aces that he had and the trump queen that he was missing. That would tell me that at worst the slam was probably hinging on a finesse. If I had an optimistic view of the hand from the point count, I probably would have gone.
The other alternative would have been for partner to bid 3♠ rather than four. That would have made it easier for me, but it would have overstated his values.
Hand #22: My hand (9 HCP; 8 losers):
♠T54 ♥AQ72 ♦K753 ♣32Partner’s hand (21 HCP; 3 losers):
♠AKQJ3 ♥4 ♦A4 ♣AK976Partner, the dealer, faced a very difficult decision. His hand met the 4×4 criterion for opening 2♣, but there were two pretty good reasons to open 1♠ instead. Many experts never use 2♣ for two-suiters. Moreover, one of partner’s suits is clubs, and it is hard to show clubs after a 2♣ opener. At any rate he opened 1♠. I bid 1NT. He jump-shifted in clubs. I vacillated between 3♠ and 4♠. Which would be stronger in this situation? I was not sure. I picked the former, and partner signed off in 4♠. I thought about going on, but I figured that my partner had no fewer than five losers.
This auction was not one of our finest moments, but we beat the two pairs that went to seven, and the two pairs that somehow found a way to lose two or three tricks.
Bergen values partner’s rock-crusher at 24 starting points. I have ten dummy points. Even before partner starts adding in distribution after he discovers our spade fit, we are in slam territory. In fact, Bergen would probably have joined the two pairs who bid the unmakeable grand. For all I know, he would have made it, too.
Hand #31: My hand (17 HCP; 5 losers):
♠Q6 ♥AKQJ852 ♦KT8 ♣QPartner’s hand (12 HCP; 8 losers):
♠A743 ♥9743 ♦A2 ♣KJ8I opened a heart. LHO liked her seven-count well enough to overcall a five-card spade suit headed by the jack. They were even vulnerable! I will try to keep this information in mind for future reference.
Partner bid 2♠. I did not think that I had enough to do anything besides sign off in 4♥.
Three pairs out of seven bid and made 6♠, which can be set with a spade lead. Two defenses found the killing lead.
LTC says that we should stop at four or five. In theory that is correct, but getting the twelfth trick only required the LHO to set down the unprotected A♣ (or any other non-spade) at trick one.
Bergen values my hand as worth 22 points as declarer. Partner has 13 points in support of hearts. From the perspective of Bergen points this one is a no-brainer. The best possible result is 6NT played by partner. I doubt, however, that too many people are going to ignore an eleven-card fit.
At this point I gave our partnership the Wienie Award. We had only played eleven hands, and three times we had been able to claim unbid slams after the first few tricks.
Hand #27: My hand (10 HCP; 7 losers):
♠AQ842 ♥A94 ♦9652 ♣7Partner’s hand (17 HCP; 6 losers):
♠K93 ♥Q8 ♦KQJ ♣AQT93No one found this slam either. After two passes LHO opened 1
♦. Partner overcalled 1NT (15-18). I transferred to spades, and we settled for the game in spades. My hand’s only exceptional feature was the singleton in clubs.
Partner had to bring in the club suit in order to score twelve tricks.
I had only 11 starter points; I was not thinking about slam. Partner gets a point for his long club suit and one each for the quality of his minor suits. All told, he has 19 dummy points. When I learn of his spade support, I can add three more points (two for the singleton plus one for the four diamonds). That gives us 33 Bergen Points, and we should have bid slam again!
Maybe this pair of hands would look like a slam to Marty Bergen, who might have consider partner’s hand as too strong for a 1NT overcall. However, my four-card suit is the one that LHO bid, and my singleton is in my partner’s long suit. Adding points for these features seems dubious. The only positive intangible is the fact that the points are all sitting between us. We needed both of those long club tricks to make twelve tricks, and that required RHO to have no clubs higher than the 10. The transportation was tricky, too.
In fact, only three out of seven pairs found all twelve tricks. One played in no trump (making four), two made only four spades, and one five.
Hand #28: My hand (10 HCP; 5 losers):
♠74 ♥KQ6543 ♦__ ♣AJT87Partner’s hand (17 HCP; 7 losers):
♠KQT9 ♥AJ8 ♦AT ♣K954I had no scruples about opening my shapely ten-count. Partner forced to game with 2♣. I rebid my hearts, and he supported. At this point I was not stopping short of slam, and we made it easily.
I was shocked when I discovered that we were the only pair that had bid the slam. LTC says that this one is in the bag as soon as partner shows support for hearts. Bergen would value my hand at 18 declarer points! The challenge for him would have been to avoid bidding the grand without the A♠.
This was a really interesting set of hands. We only bid and made one of them, but our total score was still above average. Someone who used LTC exclusively would have done better than we did, provided that they did not get carried away on hand #22. If Marty Bergen could have controlled his tendency to see thirteen tricks where there are only twelve, he would have been the overall winner.
Here is the final scorecard. The edge for Bergen Points in slam-oriented hands seems even greater in practice than in theory.
161012101012221313101×10,3×12,2×1312311112101×10,2×11,3×1211271112101012281212121012
| Hand # |
LTC |
Bergen |
Us |
Field |
Possible |
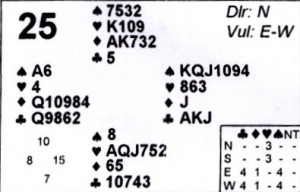 One hand at the Saturday pairs game at the Hartford Bridge club stuck in my craw. We would have done a little better if I had analyzed hand #25 correctly. I was in the West chair, and we were vulnerable. The bidding was fairly predictable up to my second bid:
One hand at the Saturday pairs game at the Hartford Bridge club stuck in my craw. We would have done a little better if I had analyzed hand #25 correctly. I was in the West chair, and we were vulnerable. The bidding was fairly predictable up to my second bid:
